
Wie stark beeinflussen menschliche Entscheidungen im Forschungsprozess die Qualität der empirischen Ergebnisse?
Wie bedeutend ist das menschliche Element für die Genauigkeit empirischer Erkenntnisse in den Wirtschaftswissenschaften? Die Unsicherheit empirischer Schätzungen wird üblicherweise als ein statistisches Phänomen betrachtet. Unbekannte Parameter einer Grundgesamtheit werden anhand einer Stichprobe geschätzt, deren Erzeugung zu so genannten Standardfehlern führt. Forschende treffen jedoch viele unbeobachtete Entscheidungen, die nicht per se richtig oder falsch sind, sich aber auf das Ergebnis der Schätzung auswirken. Beispiele hierfür sind die Wahl der Software, die Art der Datenbereinigung oder die Spezifikation der Kontrollvariablen, um nur einige zu nennen. Wir haben an einem großen crowd-basierten Feldexperiment teilgenommen, bei dem sich herausstellte, dass dieser evidenzgenerierende Prozess von Forscher zu Forscher stark variiert, wodurch eine neue Art von Unsicherheit entsteht: so genannte Nicht-Standardfehler (NSE). 164 Teams von Finanzökonominnen und Finanzökonomen testeten sechs Hypothesen an einer identischen Stichprobe von Finanzmarktdaten. Das wichtigste Ergebnis ist, dass die Nicht-Standardfehler beträchtlich sind und die gleiche Größenordnung haben wie die Standardfehler, dass sie aber nach einem anonymen Begutachtungsprozess deutlich abnehmen. Wer sich von Wirtschaftsforschern beraten lässt, sollte sich daher darüber im Klaren sein, dass die Entscheidungen der einzelnen Forschenden die empirische Evidenz mit einer nicht unerheblichen Unsicherheit behaften. Gleichzeitig scheint eine der Veröffentlichung vorausgehende Begutachtung der Ergebnisse durch wissenschaftliche Kollegen (peer-review) die Anfälligkeit für diese Art von Unsicherheit zu verringern.
23. Dezember 2022
Rat von Experten
Entscheidungsträger verlassen sich häufig auf den Rat von Experten. Diese Empfehlungen sollten auf Erkenntnissen beruhen, die aus einem transparenten und rigorosen wissenschaftlichen Protokoll resultieren. Ein bekanntes Beispiel sind Politikerinnen, die Virologinnen, Epidemiologen und andere Wissenschaftler konsultieren, um Maßnahmen zur Bekämpfung der COVID-19-Pandemie zu planen und zu beschließen. Beispiele aus dem Bereich der Wirtschaft sind Entscheidungen der Zentralbanken, ob sie ihren geldpolitischen Kurs ändern, oder des deutschen Finanzstabilitätsrats, ob makroprudenzielle Maßnahmen wie der antizyklische Kapitalpuffer aktiviert werden sollen. Diese Entscheidungen haben reale Folgen: Zinserhöhungen zur Eindämmung der Inflation wirken sich negativ auf die Wirtschaftstätigkeit aus, und höhere Eigenkapitalanforderungen an die Banken verringern das Kreditangebot für Unternehmen und Haushalte. In ihrem Bemühen um eine verantwortungsvolle Entscheidungsfindung stützt sich die Wirtschaftspolitik daher häufig auf wissenschaftliche Erkenntnisse, die von Wirtschaftswissenschaftlern erarbeitet wurden, unter Anwendung von Methoden, die in der wissenschaftlichen Gemeinschaft akzeptiert und etabliert sind. Doch wie wichtig ist der „menschliche Faktor“ bei der Gewinnung solcher Erkenntnisse? Forschende müssen bei der Durchführung empirischer Forschung mit so genannten Standard- und Nicht-Standardfehlern umgehen. Standardfehler entstehen bei der Erzeugung von Stichprobendaten. Im Gegensatz dazu resultieren Nicht-Standardfehler (NSE) aus der zusätzlichen Ungewissheit, die durch eine Reihe nicht trivialer Entscheidungen bei der Durchführung empirischer Analysen zur Generierung von Evidenz verursacht wird. So legen Ökonominnen beispielsweise ein geeignetes ökonometrisches Modell fest, bereiten die Daten für die Schätzung auf (z. B. durch Bereinigung von Ausreißern), wählen eine Programmiersprache und treffen viele weitere Entscheidungen dieser Art, wenn sie ökonomische Analysen durchführen.
Ziel des groß angelegten Feldexperiments, an dem wir teilgenommen haben, ist es, das Ausmaß von Nicht-Standardfehlern, die sich aus solchen Entscheidungen ergeben, zu messen und zu erklären. Konkret sollte das Projekt vier Fragen beantworten: 1) Wie bedeutend sind Nicht-Standardfehler für die Forschung im Bereich Finanzen?
2) Lassen sie sich im Querschnitt der Forschenden „erklären“?
3) Verringert ein anonymer Begutachtungsprozess diese Nicht-Standardfehler? 4) Sind sich die Forschenden des genauen Ausmaßes der Nicht-Standardfehler bewusst? Zu diesem Zweck wurden
164 Forschungsteams aus Finanzwissenschaftlern in einem Feldexperiment zusammengestellt, um standardisierte Analysen nach einem vorgegebenen Protokoll durchzuführen.
Die wichtigsten Ergebnisse dieses Feldversuchs sind vierfacher Art. Erstens sind die Nicht-Standardfehler erstaunlich groß, ähnlich groß wie der (mittlere) Standardfehler. Daher sollten sich die Konsumenten wirtschaftswissenschaftlicher Forschung des „menschlichen Elements“ in der Evidenz, die den Empfehlungen der Expertinnen zugrunde liegt, bewusst sein. Zweitens variieren die Nicht-Standardfehler nur geringfügig mit dem Forschungsteam, dem Arbeitsablauf und der Qualität der Forschungspapiere. Daher kann eine Erfolgsbilanz ausgewiesener Expertise oder einfach größere Erfahrung die inhärente Unsicherheit von Expertenempfehlungen nicht beseitigen. Drittens nehmen die Nicht-Standardfehler nach dem anonymen Begutachtungsprozess deutlich ab. Die strenge akademische Praxis des Peer-Review verringert also wirksam die Unsicherheit im Zusammenhang mit von Menschen erzeugter Evidenz. Anders ausgedrückt: Das bloße Vorhandensein von Nicht-Standardfehlern bedeutet nicht, dass wir unsere Entscheidungen nicht mehr auf wissenschaftliche Erkenntnisse stützen sollten – es bedeutet vielmehr, dass die Wissenschaft das am wenigsten schlechte Fundament ist, auf dem wir unsere Entscheidungen aufbauen können. Viertens werden Nicht-Standardfehler von den Beteiligten erheblich unterschätzt. Wenn also selbst die Produzenten von Forschungsergebnissen die Relevanz von Unsicherheit aufgrund idiosynkratischer Entscheidungen nicht angemessen erkennen, ist es von entscheidender Bedeutung, die Adressaten der Forschungsergebnisse noch stärker für die Grenzen wissenschaftlicher Erkenntnis und der aus ihr abgeleiteten Ratschläge zu sensibilisieren.
Nicht-Standardfehler

Wie in Abbildung 1 dargestellt, treten bei der Durchführung empirischer Forschung in allen Phasen Nicht-Standardfehler auf. Eine Quelle der Variabilität zwischen den Forschenden ist die Spezifikation des Modells. Ist das empirische Modell linear oder nicht linear? Welche Kontrollvariablen sollten einbezogen werden? Eine weitere Quelle der Variabilität liegt in der Phase der empirischen Methode. Was sind angemessene empirische Näherungswerte für die interessierenden Parameter? Welche Filter sollten auf die Stichprobe angewendet werden? Wie sollten wir Ausreißer in den Daten behandeln? Was sind geeignete Teststatistiken? Die letzte Quelle der Variabilität bezieht sich auf die Ausführungsphase. Können die Ergebnisse ohne Fehler im Programmcode reproduziert werden? In Anbetracht des Freiheitsgrads, den Forschende bei der Durchführung empirischer Forschung haben, und des Problems der Reproduzier- barkeit in der Wirtschafts- und Finanzforschung können potenzielle Nicht-Standardfehler enorm sein.
Projektentwurf
Im Kern des Projekts steht die Idee, mehrere Forschungsteams dieselben sechs Hypothesen an derselben Stichprobe aus Daten der Deutschen Börse unabhängig voneinander testen zu lassen. Die Hypothesen H1 bis H6 beziehen sich alle auf die Entwicklung der folgenden Marktmerkmale relativ zu der Nullhypothese, dass es keine Veränderung gibt: H1: Markteffizienz, H2: die realisierte Geld-Brief-Spanne, H3: der Anteil des Kundenvolumens am Gesamtvolumen,
H4: die realisierte Spanne bei Kundenaufträgen, H5: der Anteil der Marktaufträge an allen Kundenaufträgen und H6: die Brutto-Handelsumsätze der Kunden. Bei der Stichprobe handelt es sich um einen reinen Handelsdatensatz für EuroStoxx 50 Index-Futures, dem eine Agent/Prinzipal-Kennung hinzugefügt wurde. Für jeden Kauf und Verkauf ist also bekannt, ob der Marktteilnehmer auf eigene Rechnung (als Prinzipal) oder für einen Kunden (als Agent) gehandelt hat. Die Stichprobe reicht von 2002 bis 2018 und umfasst 720 Mio. Handelsdatensätze. Die einbezogenen Index-Futures gehören zu den weltweit am aktivsten gehandelten Indexderivaten. Sie bieten Anlegern ein Engagement in einem Korb von Blue-Chip-Aktien aus dem Euroraum. Mit Ausnahme des außerbörslichen Handels wird der gesamte Handel über ein elektronisches Limit-Orderbuch abgewickelt.
Die Forschungsteams werden gebeten, die Hypothesen zu testen, indem sie eine durchschnittliche jährliche Veränderung für eine selbst vorgeschlagene Messgröße schätzen, und sie werden außerdem gebeten, Standardfehler für diese Schätzungen und entsprechende t-Werte anzugeben. Im Einzelnen wird das Projekt in vier Stufen durchgeführt:
In Stufe 1 erhielten die Forschungsteams die detaillierten Anweisungen und Zugang zur Stichprobe, führten ihre Analyse durch und verfassten eine kurze wissenschaftliche Arbeit, in der sie ihre Ergebnisse vorstellten und diskutierten. Fachkollegen (Peer-Evaluatoren, PE) bewerteten diese Arbeiten. Die Evaluatoren wurden außerhalb der Gruppe der Forschenden rekrutiert, die sich als Forschungsteam angemeldet hatten.
In Stufe 2 wurden die von den Forschungsteams verfassten Papiere nach dem Zufallsprinzip gleichmäßig den PE zugeteilt, sodass jeder Beitrag zweimal bewertet wurde und jeder PE neun oder zehn Beiträge bewertete. Die PE bewerteten die Arbeiten in einem einfach-blinden Verfahren: Die PE sahen die Namen der Forschungsteams, aber nicht umgekehrt. Dies wurde allen Teilnehmenden im Voraus offengelegt. Die PE bewerteten die Arbeiten auf Ebene der Hypothesen und auf Ebene der Gesamtarbeit. Sie begründeten ihre Bewertungen in einem Feedback-Formular und wurden ermutigt, konstruktives Feedback hinzuzufügen. Die Forschungsteams erhielten dieses Feedback ungekürzt und durften ihre Ergebnisse auf dieser Grundlage aktualisieren.
Stufe 3: Nach Überarbeitung und erneuter Einreichung der Ergebnisse erhielten die Forschungsteams die fünf am besten bewerteten Arbeiten und durften ihre Ergebnisse auf der Grundlage dieser Arbeiten aktualisieren.
In Stufe 4 wurden die Teams gebeten, ihre Endergebnisse mitzuteilen, ohne die Einschränkung, einen Programmcode liefern zu müssen, der die Ergebnisse erzeugt. Diese Stufe wurde hinzugefügt, um alle Zwänge zu beseitigen und zu sehen, wie weit die Gemeinschaft der Forschungsteams einen Konsens erreichen kann. Die Konzeption des Projekts war allgemein bekannt, da sie im Voraus über eine spezielle Website kommuniziert wurde.1
Wie bedeutend sind Nicht-Standardfehler?
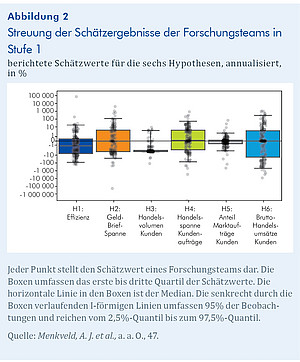
Abbildung 2 zeigt die erhebliche Streuung des Nicht-Standardfehlers (NSE) über die verschiedenen Hypothesen. Für die Effizienzhypothese (H1) beträgt der NSE 20,6%, was in etwa dem durchschnittlichen berichteten Standardfehler (SE) von 13,2% entspricht. Das Verhältnis NSE/SE beträgt 1,6. Für die Hypothese H3 beträgt das Verhältnis von NSE zu SE 1,3. Dieses Muster ergibt sich für alle Hypothesen, mit NSE/SE-Verhältnissen zwischen 0,6 und 2,1. Insgesamt zeigt das Ergebnis, dass die NSE signifikant und untersuchungswürdig sind.
Können die Nicht-Standardfehler durch Merkmale der Forschungsteams erklärt werden?
Um herauszufinden, ob verschiedene Merkmale der Forschungsteams die Größe der NSE erklären können, werden die Qualität des Teams, die Qualität des Arbeitsablaufs (approximiert durch die Reproduzierbarkeit der Ergebnisse mit Hilfe des vom Forschungsteam bereitgestellten Codes) und die durchschnittliche PE-Bewertung der Arbeiten untersucht. Die Ergebnisse deuten darauf hin, dass die Qualität des Teams, die Reproduzierbarkeit und die Qualität der Arbeiten nur schwach mit der Größe der Nicht-Standardfehler zusammenhängen. Sogar in einer Teilstichprobe, die nur Teams enthält, die bei allen Qualitätsmaßen gut abschneiden, bleiben die NSE groß.
Tragen Peer-Effekte dazu bei, Nicht-Standardfehler zu reduzieren?
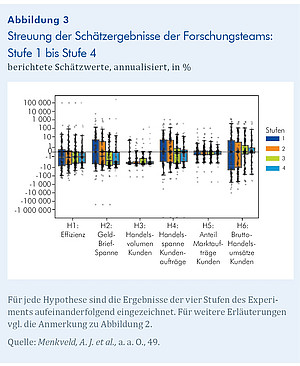
Die Forschungsteams hatten die Möglichkeit, ihre Ergebnisse zu überarbeiten, nachdem sie die Bewertung der Fachkollegen und die fünf am besten bewerteten Arbeiten erhalten hatten. Kann die zusätzliche Information aus Peer-Reviews und den bestbewerteten Arbeiten die NSE verringern? Abbildung 3 zeigt die Konvergenz der NSE aus den von den Teams gemeldeten Schätzungen im Verlauf der Stufen des Projekts. Insgesamt verringern sich die NSE von der ersten bis zur letzten Stufe um etwa 53,5%. Der Rückgang ist relativ gleichmäßig über die drei Stufen verteilt. Nachdem die Teams in der zweiten Stufe von zwei PE ein schriftliches Feedback zu ihrer Arbeit erhalten haben, sinkt der Nicht-Standardfehler um 14,5%. In der dritten Stufe, nachdem die Teams die besten fünf Arbeiten gesehen haben, schrumpft er um weitere 20%, und in der letzten Phase, wenn die Forschungsteams ihre uneingeschränkten Schätzungen einreichen, um weitere 19%. Diese Ergebnisse deuten darauf hin, dass Peer-Effekte dazu beitragen, die NSEs deutlich zu reduzieren.
Sind sich die Forschenden über das Ausmaß der Nicht-Standardfehler im Klaren?

Die Forschungsteams wurden auch gebeten, am Ende der ersten Stufe ihre Vermutung bezüglich der Höhe der NSE für jede Hypothese anzugeben. Es ist naheliegend zu untersuchen, ob sich die Forschenden des Ausmaßes der NSE bewusst sind. Abbildung 4 zeigt die Verteilung der gemeldeten Vermutungen und die tatsächlichen Werte, die durch orange Punkte dargestellt sind. Die überwiegende Mehrheit der Teams hat die Streuung unterschätzt: Der durch die Kästchen gekennzeichnete Interquartilsbereich liegt durchweg unterhalb des orangen Punktes.
Schlussfolgerungen
Die Entscheidungsfindung in modernen Gesellschaften stützt sich in hohem Maße auf den Rat von Expertinnen und Experten, der sich häufig auf wissenschaftliche Erkenntnisse stützt. Vor allem in der Wirtschafts- und Finanzpolitik wurden immer mehr Verfahren zur Erleichterung einer evidenzbasierten Entscheidungsfindung eingeführt, z. B. strukturierte Ansätze für Ex-post-Evaluierungen der Politik durch den Rat für Finanzstabilität oder die Einbeziehung von akademischen Wirtschaftswissenschaftlern in die Gestaltung und Umsetzung der Geldpolitik.
Forschende haben jedoch bei der Durchführung empirischer Analysen einen erheblichen Freiheitsgrad, z. B. bei der Modellspezifikation, der Datenbereinigungsmethode, der Softwareauswahl und einer Fülle ähnlicher Entscheidungen. Daraus ergibt sich eine inhärente Unsicherheit der empirischen Daten, die auf die Entscheidungen der Forscher bei der Durchführung von Analysen zurückzuführen ist. Dieses große Feldexperiment, das von 164 Forschungsteams aus erfahrenen Finanzwissenschaftlern durchgeführt wurde, zielte darauf ab, die daraus resultierenden Nicht-Standardfehler zu quantifizieren.
Das wichtigste Ergebnis dieses Experiments ist, dass die Nicht-Standardfehler eine ähnliche Größenordnung erreichen wie die Standardfehler. Anders ausgedrückt: Die Unsicherheit empirischer Daten, die auf statistische Ungenauigkeit zurückzuführen ist, ist vergleichbar mit der Unsicherheit, die durch den menschlichen Faktor bei der Durchführung von Forschungsarbeiten entsteht. Daher sind die Konsumenten ökonomischer Forschung gut beraten, sich bewusst zu machen, dass auch wirtschaftswissenschaftliche Erkenntnisse mit einer gewissen Unsicherheit behaftet sind, die auf die Entscheidungen der Forschenden zurückzuführen ist – unabhängig davon, wie erfahren diese sind und wie erfolgreich sie in der Vergangenheit waren. Wichtig ist jedoch, dass Peer-Reviews die Unsicherheit aufgrund von Nicht-Standardfehlern verringern. Folglich sind Ratschläge an Entscheidungsträger, die auf strenger akademischer Forschung beruhen, zwar keine Garantie für eine unumstößliche „Wahrheit“ und sollten mit Vorsicht und Bedacht konsumiert werden, aber sie übertrumpfen eindeutig Empfehlungen, die aus weniger strengen, eher meinungsbetonten Prozessen abgeleitet werden.
Endnoten
1 Für nähere Informationen siehe https://fincap.academy.





