Inhalt
Seite 1
Rat von ExpertenSeite 2
ProjektentwurfSeite 3
Tragen Peer-Effekte dazu bei, Nicht-Standardfehler zu reduzieren?Seite 4
Endnoten Auf einer Seite lesenProjektentwurf
Im Kern des Projekts steht die Idee, mehrere Forschungsteams dieselben sechs Hypothesen an derselben Stichprobe aus Daten der Deutschen Börse unabhängig voneinander testen zu lassen. Die Hypothesen H1 bis H6 beziehen sich alle auf die Entwicklung der folgenden Marktmerkmale relativ zu der Nullhypothese, dass es keine Veränderung gibt: H1: Markteffizienz, H2: die realisierte Geld-Brief-Spanne, H3: der Anteil des Kundenvolumens am Gesamtvolumen,
H4: die realisierte Spanne bei Kundenaufträgen, H5: der Anteil der Marktaufträge an allen Kundenaufträgen und H6: die Brutto-Handelsumsätze der Kunden. Bei der Stichprobe handelt es sich um einen reinen Handelsdatensatz für EuroStoxx 50 Index-Futures, dem eine Agent/Prinzipal-Kennung hinzugefügt wurde. Für jeden Kauf und Verkauf ist also bekannt, ob der Marktteilnehmer auf eigene Rechnung (als Prinzipal) oder für einen Kunden (als Agent) gehandelt hat. Die Stichprobe reicht von 2002 bis 2018 und umfasst 720 Mio. Handelsdatensätze. Die einbezogenen Index-Futures gehören zu den weltweit am aktivsten gehandelten Indexderivaten. Sie bieten Anlegern ein Engagement in einem Korb von Blue-Chip-Aktien aus dem Euroraum. Mit Ausnahme des außerbörslichen Handels wird der gesamte Handel über ein elektronisches Limit-Orderbuch abgewickelt.
Die Forschungsteams werden gebeten, die Hypothesen zu testen, indem sie eine durchschnittliche jährliche Veränderung für eine selbst vorgeschlagene Messgröße schätzen, und sie werden außerdem gebeten, Standardfehler für diese Schätzungen und entsprechende t-Werte anzugeben. Im Einzelnen wird das Projekt in vier Stufen durchgeführt:
In Stufe 1 erhielten die Forschungsteams die detaillierten Anweisungen und Zugang zur Stichprobe, führten ihre Analyse durch und verfassten eine kurze wissenschaftliche Arbeit, in der sie ihre Ergebnisse vorstellten und diskutierten. Fachkollegen (Peer-Evaluatoren, PE) bewerteten diese Arbeiten. Die Evaluatoren wurden außerhalb der Gruppe der Forschenden rekrutiert, die sich als Forschungsteam angemeldet hatten.
In Stufe 2 wurden die von den Forschungsteams verfassten Papiere nach dem Zufallsprinzip gleichmäßig den PE zugeteilt, sodass jeder Beitrag zweimal bewertet wurde und jeder PE neun oder zehn Beiträge bewertete. Die PE bewerteten die Arbeiten in einem einfach-blinden Verfahren: Die PE sahen die Namen der Forschungsteams, aber nicht umgekehrt. Dies wurde allen Teilnehmenden im Voraus offengelegt. Die PE bewerteten die Arbeiten auf Ebene der Hypothesen und auf Ebene der Gesamtarbeit. Sie begründeten ihre Bewertungen in einem Feedback-Formular und wurden ermutigt, konstruktives Feedback hinzuzufügen. Die Forschungsteams erhielten dieses Feedback ungekürzt und durften ihre Ergebnisse auf dieser Grundlage aktualisieren.
Stufe 3: Nach Überarbeitung und erneuter Einreichung der Ergebnisse erhielten die Forschungsteams die fünf am besten bewerteten Arbeiten und durften ihre Ergebnisse auf der Grundlage dieser Arbeiten aktualisieren.
In Stufe 4 wurden die Teams gebeten, ihre Endergebnisse mitzuteilen, ohne die Einschränkung, einen Programmcode liefern zu müssen, der die Ergebnisse erzeugt. Diese Stufe wurde hinzugefügt, um alle Zwänge zu beseitigen und zu sehen, wie weit die Gemeinschaft der Forschungsteams einen Konsens erreichen kann. Die Konzeption des Projekts war allgemein bekannt, da sie im Voraus über eine spezielle Website kommuniziert wurde.1
Wie bedeutend sind Nicht-Standardfehler?
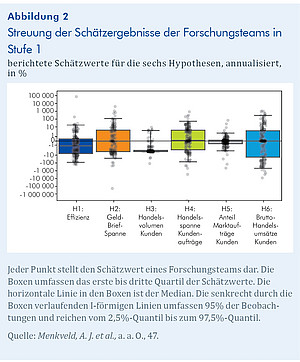
Abbildung 2 zeigt die erhebliche Streuung des Nicht-Standardfehlers (NSE) über die verschiedenen Hypothesen. Für die Effizienzhypothese (H1) beträgt der NSE 20,6%, was in etwa dem durchschnittlichen berichteten Standardfehler (SE) von 13,2% entspricht. Das Verhältnis NSE/SE beträgt 1,6. Für die Hypothese H3 beträgt das Verhältnis von NSE zu SE 1,3. Dieses Muster ergibt sich für alle Hypothesen, mit NSE/SE-Verhältnissen zwischen 0,6 und 2,1. Insgesamt zeigt das Ergebnis, dass die NSE signifikant und untersuchungswürdig sind.
Können die Nicht-Standardfehler durch Merkmale der Forschungsteams erklärt werden?
Um herauszufinden, ob verschiedene Merkmale der Forschungsteams die Größe der NSE erklären können, werden die Qualität des Teams, die Qualität des Arbeitsablaufs (approximiert durch die Reproduzierbarkeit der Ergebnisse mit Hilfe des vom Forschungsteam bereitgestellten Codes) und die durchschnittliche PE-Bewertung der Arbeiten untersucht. Die Ergebnisse deuten darauf hin, dass die Qualität des Teams, die Reproduzierbarkeit und die Qualität der Arbeiten nur schwach mit der Größe der Nicht-Standardfehler zusammenhängen. Sogar in einer Teilstichprobe, die nur Teams enthält, die bei allen Qualitätsmaßen gut abschneiden, bleiben die NSE groß.






